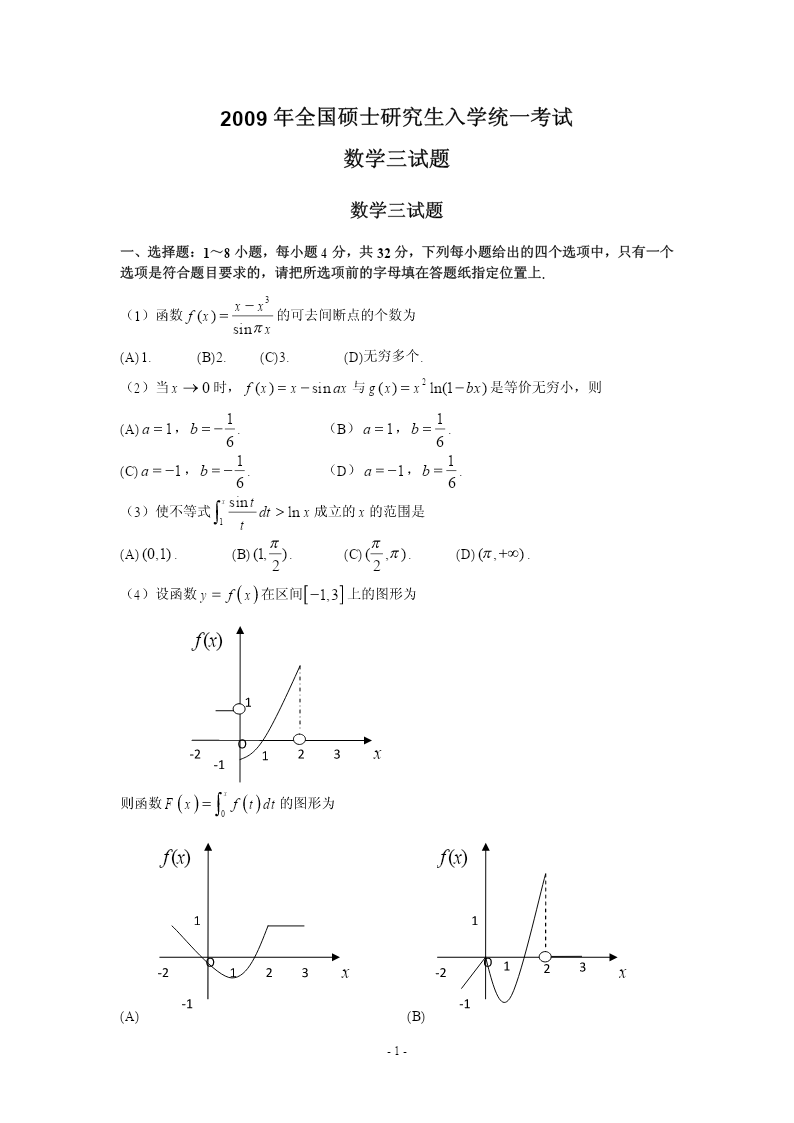
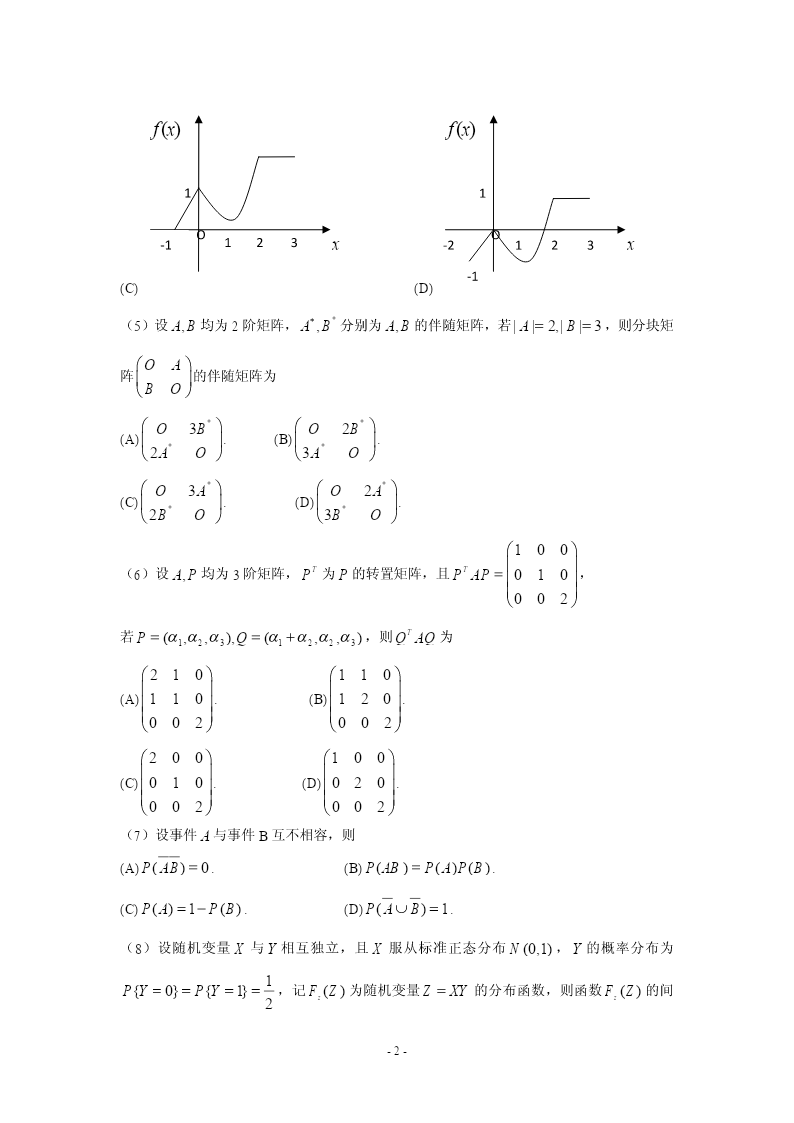
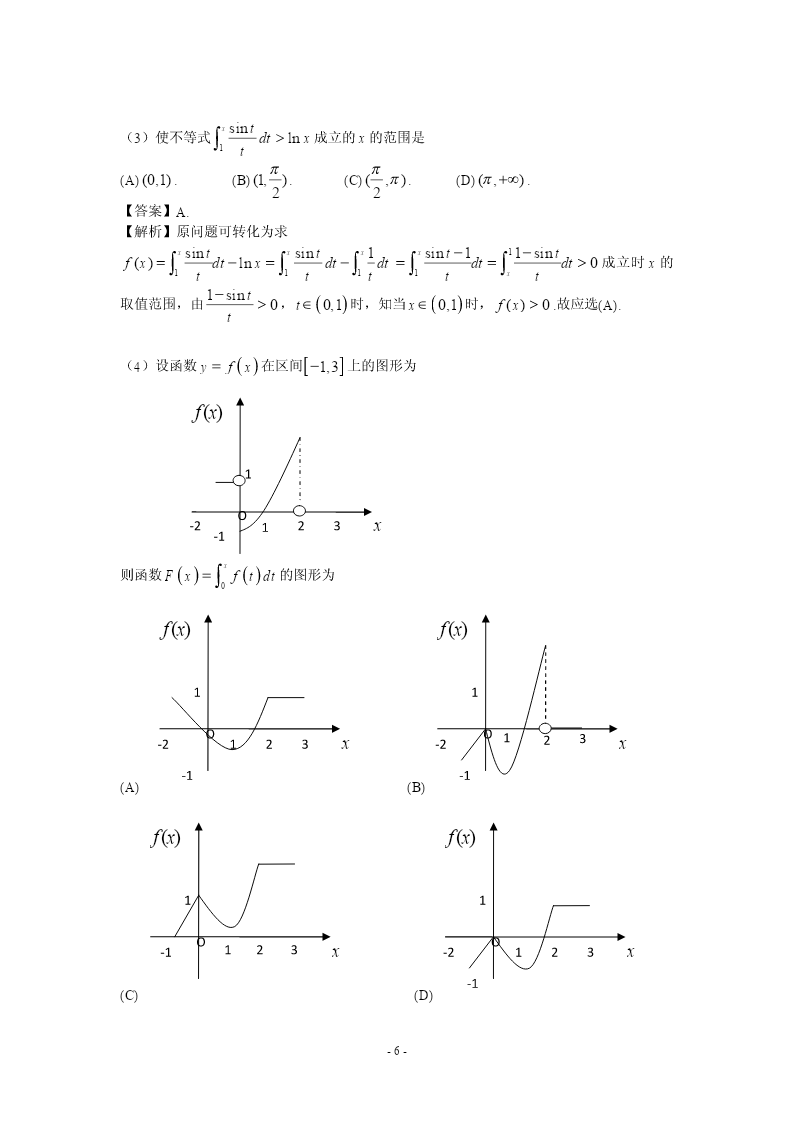
2009年全国硕士研究生入学统一考试数学三试题数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.xx3（1）函数f()x的可去间断点的个数为sinx(A)1.(B)2.(C)3.(D)无穷多个.（2）当x0时，f(x)xsinax与g(x)x2ln(1bx)是等价无穷小，则11(A)a1，b.（B）a1，b.6611(C)a1，b.（D）a1，b.66xsint（3）使不等式dtlnx成立的x的范围是1t(A)(0,1).(B)(1,).(C)(,).(D)(,).22（4）设函数yfx在区间1,3上的图形为f()x1O-2123x-1x则函数Fxftdt的图形为0f()xf()x11OO-2123x-2123x-1-1(A)(B)-1-f()xf()x11OO-1123x-2123x-1(C)(D)（5）设AB,均为2阶矩阵，AB,*分别为AB,的伴随矩阵，若|AB|2,||3，则分块矩OA阵的伴随矩阵为BOOB3*OB2*(A).(B).**2AO3AOOA3*OA2*(C).(D).**2BO3BO100TT（6）设AP,均为3阶矩阵，P为P的转置矩阵，且PAP010，002T若PQ(1,2,3),(12,2,3)，则QAQ为210110(A)110.(B)120.002002200100(C)010.(D)020.002002（7）设事件A与事件B互不相容，则(A)P(AB)0.(B)P()()()ABPAPB.(C)PAPB()1().(D)PAB()1.（8）设随机变量X与Y相互独立，且X服从标准正态分布N(0,1)，Y的概率分布为1PYPY{0}{1}，记FZ()为随机变量ZXY的分布函数，则函数FZ()的间2zz-2-断点个数为(A)0.(B)1.(C)2.(D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.eecosx（9）lim.x031x21z（10）设z()xeyx，则.x(1,0)en(1)n（11）幂级数xn的收敛半径为.2n1n（12）设某产品的需求函数为QQP(),其对应价格P的弹性p0.2，则当需求量为10000件时，价格增加1元会使产品收益增加元.300TTT（13）设(1,1,1),(1,0,k)，若矩阵相似于000，则k.0002(14)设X1，X2,…,Xn为来自二项分布总体B(,)np的简单随机样本，X和S分别为样本均值和样本方差，记统计量TXS2，则ET.三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数f(x,y)x22y2ylny的极值.（16）（本题满分10分）1x计算不定积分ln(1)dx(x0).x（17）（本题满分10分）计算二重积分()xydxdy，其中D{(x,y)(x1)2(y1)22,yx}.D（18）（本题满分11分）（Ⅰ）证明拉格朗日中值定理，若函数f()x在a,b上连续，在a,b上可导，则a,b，得证f()()()bfaf'ba.（Ⅱ）证明：若函数f()x在x0处连续，在0,,(0)内可导，且limf'(x)A，x0''则f(0)存在，且f(0)A.-3-（19）（本题满分10分）设曲线yf()x，其中f()x是可导函数，且f(x)0.已知曲线yf()x与直线y0,x1及xt(t1)所围成的曲边梯形绕x轴旋转一周所得的立体体积值是该曲边梯形面积值的t倍，求该曲线的方程.（20）（本题满分11分）1111设A=111,1.104222（Ⅰ）求