 预览加载中,请您耐心等待几秒...
预览加载中,请您耐心等待几秒...

1/10

2/10

3/10

4/10

5/10
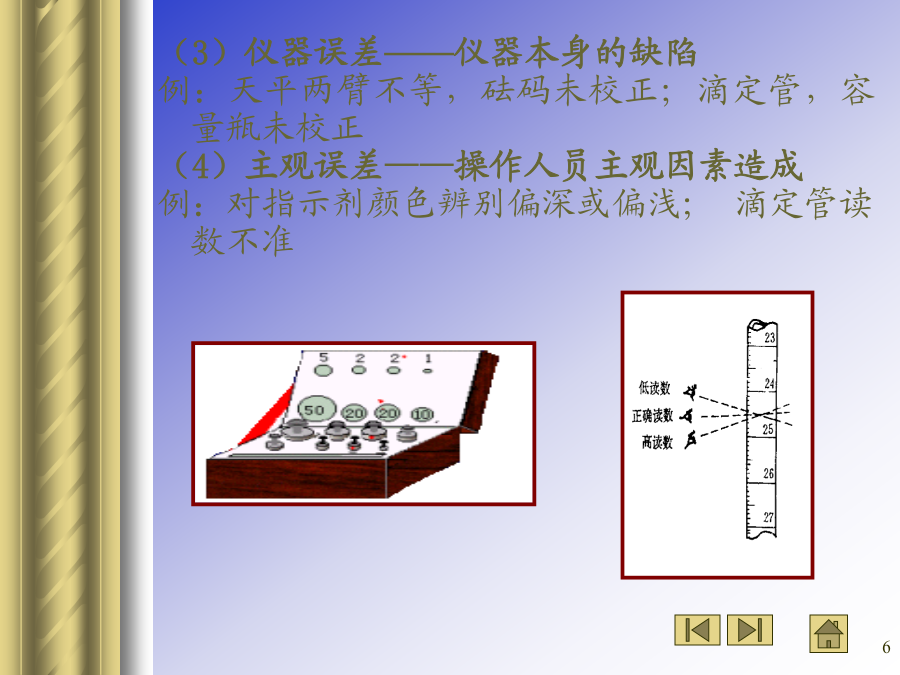
6/10

7/10

8/10

9/10

10/10
亲,该文档总共49页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
如果您无法下载资料,请参考说明:
1、部分资料下载需要金币,请确保您的账户上有足够的金币
2、已购买过的文档,再次下载不重复扣费
3、资料包下载后请先用软件解压,在使用对应软件打开
第五章误差及数据处理§2-1定量分析中的误差三、准确度和精密度的关系§2-2误差产生的原因及其减免方法2.产生的原因:(1)方法误差——选择的方法不够完善例:重量分析中沉淀的溶解损失,滴定分析中指示剂选择不当(2)试剂误差——所用试剂有杂质例:去离子水不合格;试剂纯度不够(3)仪器误差——仪器本身的缺陷例:天平两臂不等,砝码未校正;滴定管,容量瓶未校正(4)主观误差——操作人员主观因素造成例:对指示剂颜色辨别偏深或偏浅;滴定管读数不准二、随机误差(偶然误差)1.特点:(1)不恒定,无法校正;(2)服从正态分布规律:大小相近的正误差和负误差出现的几率机等;小误差出现的频率较高,而大误差出现的频率较低,很大误差出现的几率近于零。2.产生的原因:(1)偶然因素(室温,气压的微小变化);(2)个人辩别能力(滴定管读数)注意:过失误差属于不应有的过失。三、误差的减免(一)系统误差的减免1.方法误差——采用标准方法作对照试验2.仪器误差——校准仪器3.试剂误差——作空白试验(二)随机误差的减免——增加平行测定的次数,取其平均值,可以减少随机误差。§2-3分析结果的数据处理(二)标准偏差标准偏差又称均方根偏差,标准偏差的计算分两种情况:1.当测定次数趋于无穷大时,总体标准偏差:2.有限测定次数样本标准偏差:S:有限次测定的标准偏差n:测定次数表2-1t值表(t:某一置信度下的几率系数)§2-4分析测试结果准确度的评价可疑数据的取舍—过失误差的判断1.Q检验法步骤:(1)数据从小至大排列x1,x2,……,xn(2)求极差xn-x1(3)确定检验端:比较可疑数据与相邻数据之差xn-xn-1与x2-x1,先检验差值大的一端(4)计算:(5)根据测定次数和要求的置信度(如90%)查表:2.格鲁布斯(Grubbs)检验法步骤:(1)数据从小至大排列x1,x2,……,xn(2)计算该组数据的平均值和标准偏差S(3)确定检验端:比较可疑数据与平均值之差-x1与xn-,先检验差值大的一端(4)计算:(5)根据测定次数和要求的置信度(如95%)查表:(3)查表(F表),比较:若F计>F表,说明两组数据的精密度存在显著性差异若F计<F表,说明两组数据的精密度无显著性差异,再用t检验法检验两组数据的准确度有无显著性差异。212.t检验法分析方法准确度的检验—系统误差的判断(1)平均值与标准值()的比较a.计算t值(2)两组数据的平均值比较(同一试样)新方法与经典方法(标准方法)测定的两组数据两个分析人员测定的两组数据两个实验室测定的两组数据a.求合并的标准偏差:数据的检验解决两类问题:1.可疑数据的取舍—过失误差的判断三、分析结果的质量保证1.质量保证和质量控制质量保证是指保证工作质量所必须具备的条件和措施,包括人员素质、实验室仪器设备条件、环境条件及技术管理制度。质量控制是指为保证实验室中得到的数据的准确度和精密度能够落在已知概率限度内所采取的措施。§2-5有效数字及其运算规则2.数字零在数据中具有双重作用:(1)若作为普通数定使用,是有效数字如0.31804位有效数字3.18010-1(2)若只起定位作用,不是有效数字。如0.03183位有效数字3.1810-23.改变单位不改变有效数字的位数:如19.02mL为19.0210-3L4.注意点(1)容量器皿;滴定管;移液管;容量瓶;4位有效数字(2)分析天平(万分之一)取4位有效数字(3)标准溶液的浓度,用4位有效数字表示:0.1000mol/L(4)pH4.34,小数点后的数字位数为有效数字位数对数值,lgX=2.38;lg(2.4102)二、有效数字的运算规则1.加减运算:几个数据相加或相减时,它们的和或差的有效数字的保留,应依小数点后位数最少的数据为根据,即取决于绝对误差最大的那个数据。2.乘除运算:3.整化原则:(在取舍有效数字位数时,应注意以下几点)(1)在分析化学计算中,经常会遇到一些分数、整数、倍数等,这些数可视为足够有效。(2)若某一数据第一位有效数字等于或大于8,则有效数字的位数可多算一位。如:9.98,按4位算。(3)在计算结果中,可根据四舍五入原则(最好采用“四舍六入五留双”原则)进行整化。(4)有关化学平衡计算中的浓度,一般保留二位或三位有效数字。pH值的小数部分才为有效数字,一般保留一位或二位有效数字。例如,[H+]=5.210-3mol·L-1,则pH=2.28(5)表示误差时,取一位有效数字已足够,最多取二位。三、有效数字规则在
















