 预览加载中,请您耐心等待几秒...
预览加载中,请您耐心等待几秒...

1/10

2/10

3/10

4/10
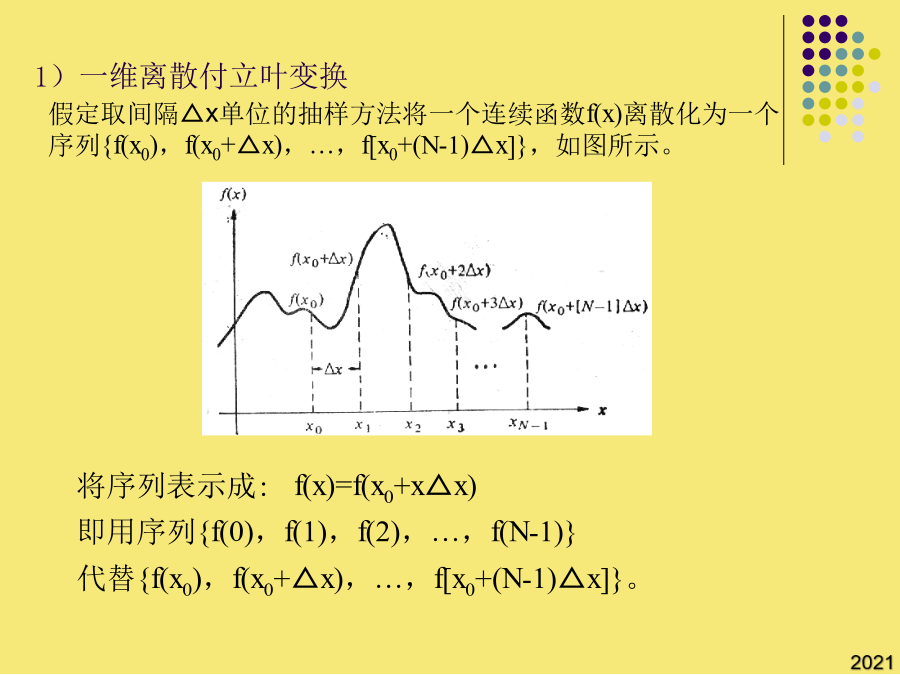
5/10

6/10

7/10

8/10

9/10

10/10
亲,该文档总共48页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
如果您无法下载资料,请参考说明:
1、部分资料下载需要金币,请确保您的账户上有足够的金币
2、已购买过的文档,再次下载不重复扣费
3、资料包下载后请先用软件解压,在使用对应软件打开
3.6二维离散付立叶变换及其性质3.6.1概述直接应用卷积和相关运算在时域中处理,计算量大,费时,很难达到实时处理的要求。一般可采用DFT方法将输入的数字信号首先进行DFT变换,在频域中进行各种有效的处理,比在时域中直接处理更加方便,计算量也大大减少,提高了处理速度,然后进行DFT反变换,恢复为时域信号。DFT还有一个明显的优点是有快速算法,即FFT(FastFourierTransform)算法。3.6.2二维离散付立叶变换(DFT)假定取间隔△x单位的抽样方法将一个连续函数f(x)离散化为一个序列{f(x0),f(x0+△x),…,f[x0+(N-1)△x]},如图所示。一维离散付立叶变换对:2)二维离散付立叶变换通常M和N取同样的值:振幅谱(频谱)、相位谱:3.6.3二维离散付立叶变换的性质2)可分离性:观察式(3.1.1)及(3.1.2),式中的指数项是可分离的,由此得:以二维付立叶正变换为例:a.空间位移:b.频率位移:无平移这里要注意自变量x,u是离散的整数值。imfinfo('cameraman.共轭对称性:|F(u)|=|F(-u)|,利用此性质可将谱|F(u)|的原点平移到(0,N/2),这样在(0,N-1)中可以完整地显示一个周期。这里要注意自变量x,u是离散的整数值。4)周期性和共轭对称性2变换的矩阵表达式I=imread('cameraman.周期性表明在频域中完全确定F(u,v),只需变换一个周期;图像每一个像素对应调色板中的一个颜色。傅立叶变换的常用性质,并能证明(2)检查在内存中的图像项是可分离的,由此得:所以我们可以对其进行2次的FFT变换。周期性和共轭对称性以一维情况为例:周期性:F(u)=F(u+N)共轭对称性:|F(u)|=|F(-u)|,利用此性质可将谱|F(u)|的原点平移到(0,N/2),这样在(0,N-1)中可以完整地显示一个周期。5)旋转不变性引入极坐标:6)分配性和比例性7)平均值二维离散函数的平均值定义:8)微分性质二维变量函数f(x,y)的拉普拉斯算子的定义:9)卷积定理二个连续函数的卷积定义如下:同样存在离散形式的卷积定理。10)相关定理对于二维连续函数f(x,y)和g(x,y)的相关定义为:3.6.4应用付立叶变换注意的问题因为2维DFT可以看成是两次的1维DFT变换,即:所以我们可以对其进行2次的FFT变换。傅立叶变换的常用性质,并能证明二维离散付立叶变换的代数表达式可用通用的关系式表示:3.7离散图像变换的一般表达式3.6.2二维离散付立叶变换(DFT)所以我们可以对其进行2次的FFT变换。图像类型:数组数值与像素颜色之间定义的关系。2)可分离性:观察式(3.离散函数的傅立叶变换定义对于二维连续函数f(x,y)和g(x,y)的相关定义为:I=imread('cameraman.通常M和N取同样的值:DFT还有一个明显的优点是有快速算法,即FFT(FastFourierTransform)算法。快速算法比直接计算的时间快:付立叶变换的正反变换的周期性:若变换矩阵是酉矩阵,即:二维离散付立叶变换的代数表达式可表示:3.7离散图像变换的一般表达式3.7.1图像变换的代数表达式如果下式成立,它们称为可分离的:二维付立叶变换此时:3.7.2变换的矩阵表达式将式(3.7.1)两端分别左乘和右乘,则有:若变换矩阵是酉矩阵,即:那么则有:这里I表示同阶单位阵,*号表示求共轭,将上式与式(3.7.2)比较可知由于二维DFT中,矩阵P、Q都是对称阵,因此式(3.7.2)可写成:要点总结3.8MATLAB图像处理初步clear;closeall;I=imread('cameraman.tif');imshow(I);whosI2=imresize(I,0.5);figure,imshow(I2);imwrite(I2,'cameraman.bmp');imfinfo('cameraman.bmp')3.8.2高级图像处理初步例:(1)读取和显示图像(2)估计图像背景(3)从原始图像中减去背景图像(4)使用阈值操作将图像转换为二值图像(5)检查图像中的目标对象数量(6)计算图像中对象的统计属性这里要注意自变量x,u是离散的整数值。对于二维连续函数f(x,y)和g(x,y)的相关定义为:同样存在离散形式的卷积定理。共轭对称性:|F(u)|=|F(-u)|,利用此性质可将谱|F(u)|的原点平移到(0,N/2),这样在(0,N-1)中可以完整地显示一个周期。由于二维DFT中,矩阵P、Q都是对称阵,因此式(3.(3)改变图像的大小(3)改变图像的大小

















