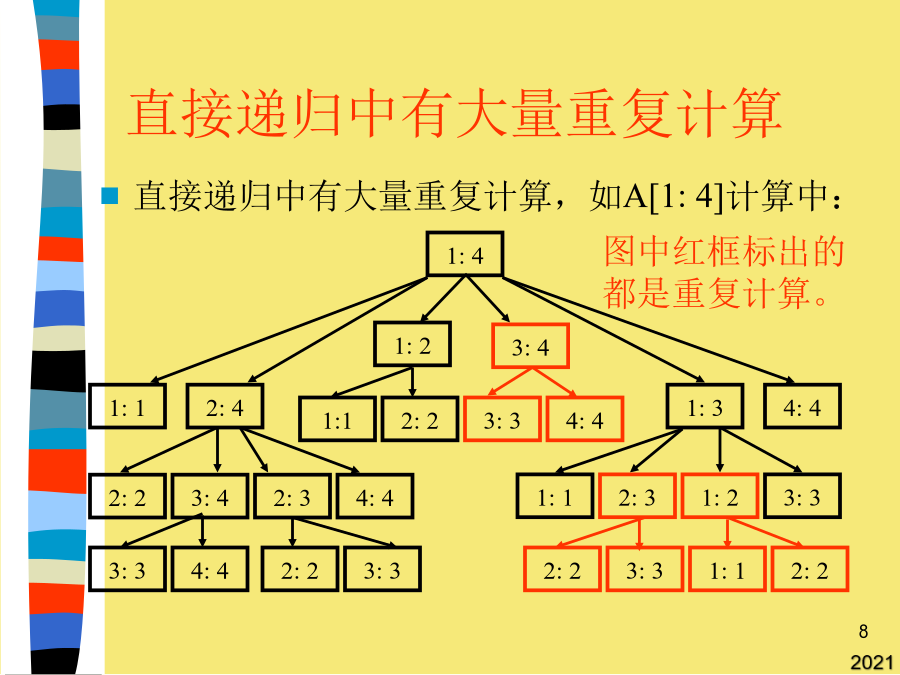
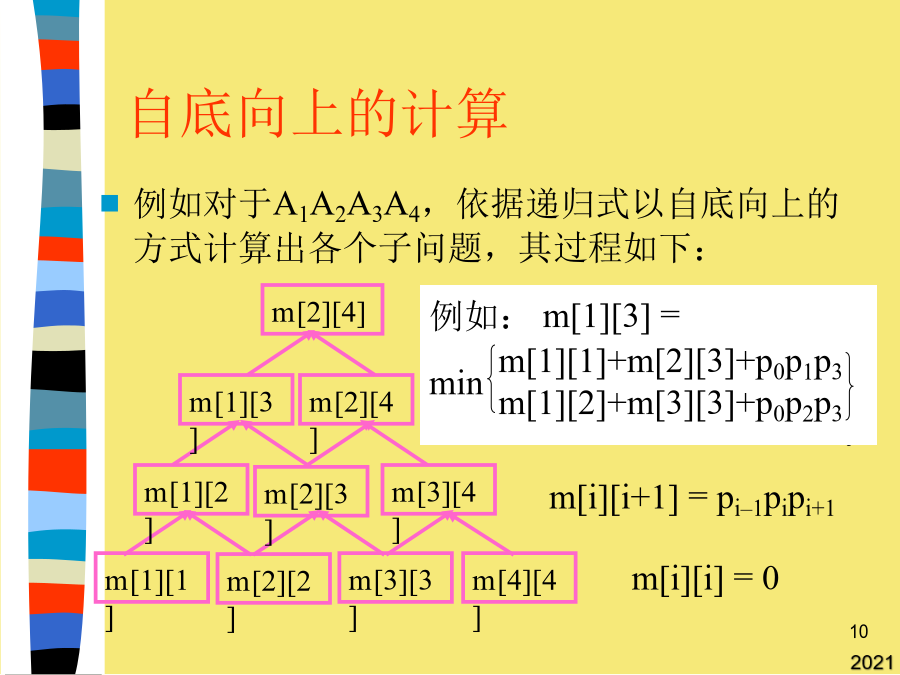
第四章动态规划矩阵连乘问题不同计算顺序的差别不同计算顺序的数量分解最优解的结构建立递归关系直接递归的时间复杂性直接递归中有大量重复计算消除重复的计算自底向上的计算消除重复的矩阵连乘算法MatrixChain的运行举例MatrixChain的时间复杂性动态规划的基本思想动态规划的基本要素动态规划的基本方法动态规划的备忘录方法凸多边形最优三角剖分这样就可以用填表保存子问题解的方法来提高效率。相应于此权函数的最优三角剖分即为最小弦长三角剖分。若按((A1A2)A3)来计算，则需要的数乘次数为10×100×5+10×5×50=7500或者，I(m,n)=I(m,n–1)–rintt=m[i][k]+m[k+1][j]+p[i–1]*p[k]*p[j];这样就可以用填表保存子问题解的方法来提高效率。确定一种连乘的顺序，使得矩阵连乘的计算量为最小。op[1],v[1],op[2],v[2],…,op[n],v[n]=1+(n–1)+∑(T(k)+T(n–k))k=1k=1VoidMinWeightTriangulation(intn,Type**t,int**s)1≤s≤j当i=j时，A[i,j]为单一矩阵，m[i][j]=0；游戏的第1步，将一条边删去；I[i][0]=S[i][0]–q;}D(i–1,0)–rfori0三角剖分问题和矩阵连乘积问题都对应于一个完全二叉树，也称为表达式的语法树。最优子结构性质最优三角剖分的递归结构最优三角剖分的算法多边形游戏多边形游戏的表达多边形游戏的最优子结构性质多边形游戏的最优子结构分析多边形游戏的递归求解I(0,j)fori0设n个矩阵的连乘积有P(n)个不同的计算顺序。凸多边形的三角剖分是将一个凸多边形分割成互不相交的三角形的弦的集合T。这样就可以用填表保存子问题解的方法来提高效率。每个子问题初始化时都标记为尚未求解。123456VoidMinWeightTriangulation(intn,Type**t,int**s)for(intj=1;j<=n;j++)S[0][0]=0;D[0][0]=–q;I[0][0]=–q因此整个计算过程中应同时计算最大值和最小值。了给m[i][j]赋初值。游戏的第1步，将一条边删去；intS[m][n],D[m][n],I[m][n];I(0,j–1)–rforj0设A和B分别是p×q和q×r的两个矩阵，则乘积C=AB为p×r的矩阵，计算量为pqr次数乘。k=1求解多边形游戏的递归式多边形游戏的动态规划算法DNA序列的相似性DNA序列的相似性递归求序列相似性递归求序列相似性递归求序列相似性递归求序列相似性动态规划求序列相似性动态规划法的递归式=1+(n–1)+∑(T(k)+T(n–k))I(0,j–1)–rforj0intu=t[i][k]+t[k+1][j]+w(i–1,k,j);输出S(m,n);{for(inti=1;i<=n;i++)t[i][i]=0;对于长度为k的空位，其得分为–(q+kr)。执行第(7)句计算A[2:3][4:4]，t=m[2][3]+m[4][4]+p[1]*p[3]*p[4]=2625+0+35*5*10=4375＜6000，所以m[2][4]改为4375，断点改为3。当i＜j时，利用最优子结构性质有：定义t[i][j],1≤i<j≤n,为子多边形{vi–1,vi,…,vj}的最优三角剖分所对应的权函数值，并为方便起见，设退化的多边形{vi–1,vi}的权值为0。可定义三角形上各种各样的权函数w。当以后遇到该子问题时即可查表取出其解，避免了重复计算。S(i,0)–qfori0AGCTACGTACACTACC递归式中的数据依赖递归式中的数据依赖初始化的工作S[i,j]、D[i,j]和I[i,j]的计算动态规划总结