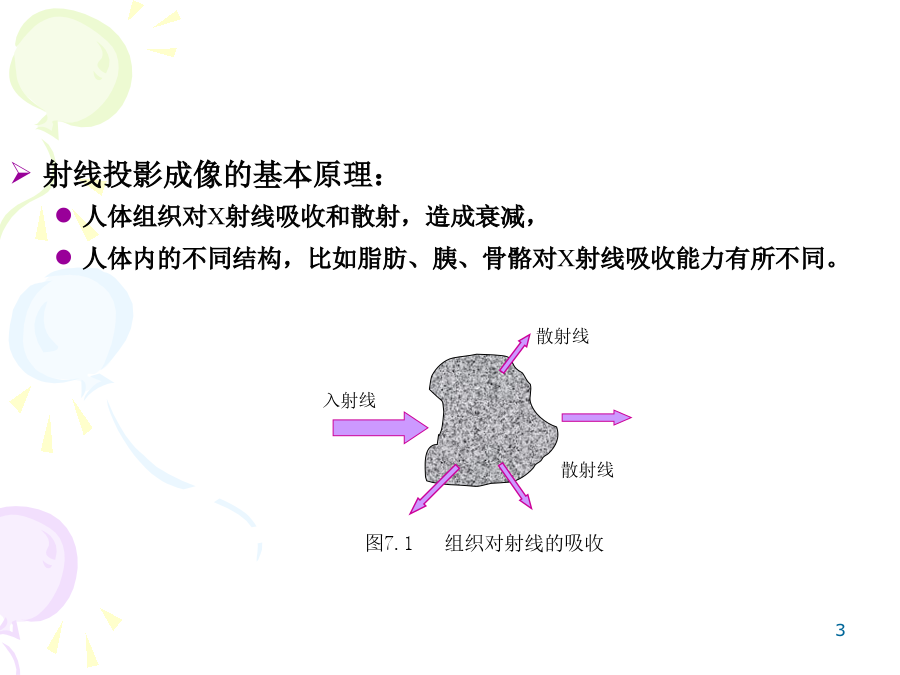
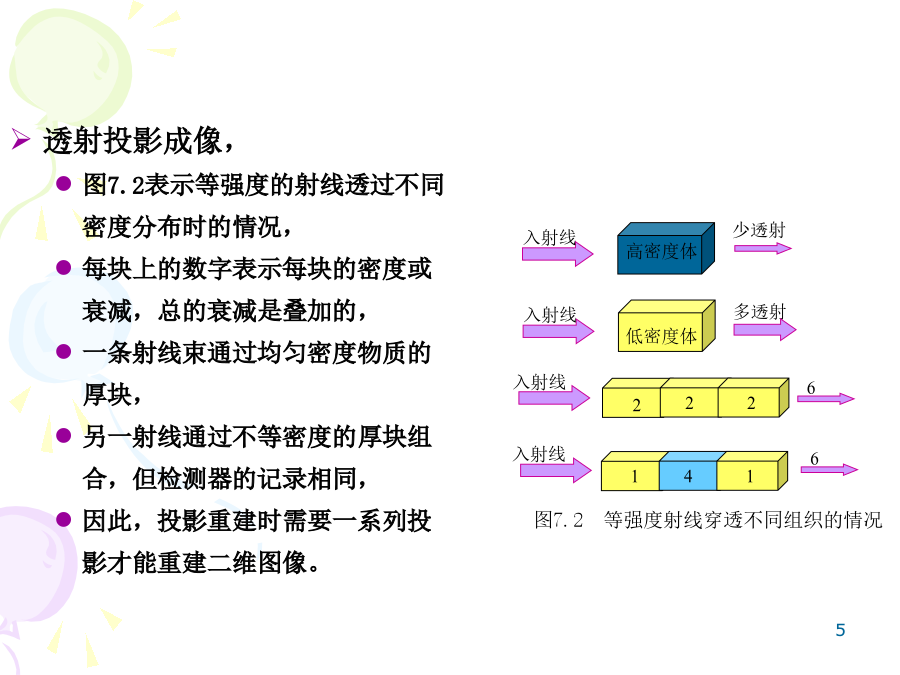
第7章图像重建图像重建：由一系列沿直线投影图来重建二维图像，由一系列二维图像重建三维物体。成像方式：透射断层成像发射断层成像反射断层成像射线种类：X射线成像、核磁共振成像、正电子发射成像、超声成像、微波成像、激光共焦成像、……射线投影成像的基本原理：人体组织对X射线吸收和散射，造成衰减，人体内的不同结构，比如脂肪、胰、骨骼对X射线吸收能力有所不同。投射断层成像：射线穿过物体，在检测器上得到的遭受衰减的值＝＝射线的投影，根据投影可以了解物体对射线的吸收程度。发射断层成像：发射源在物体内部，将具有放射性的离子（放射元素）注入物体内部，在物体外部检测其经过物体吸收之后放射量。反射断层成像：将入射信号（通常是单色平面波）入射到物体上，通过检测经物体散射（反射）后的信号强度来重建。7.1计算机断层扫描技术医学影像领域：ComputedTomography(CT)：获1979年诺贝尔奖（NobelPrice）布尔赫、珀塞尔，获1952年诺贝尔奖，发现了核磁共振现象劳特布尔（美）、P·曼斯菲尔德（英）获2003年年诺贝尔奖，核磁共振的研究第一次直线平移扫描完毕后，扫描系统旋转一个小角度，再作第二次直线式平移扫描，获得另一组投影数据；重复以上过程，便得到很多组投影数据；对这些数据进行处理形成三维图像。7.2投影定理将投影式(7.6)只对s1作一维傅立叶变换，将指数项作变换，得投影定理（切片定理）：f(x,y)在一条与x轴夹角为θ，离开原点距离为r的直线上的投影的傅立叶变换＝＝二维傅立叶变换在与u轴成θ方向上的切片三维图像重建基础：若投影变换G(r,θ)中对所有的r和θ值都已知，则图像的二维傅立叶变换也可以完全确定，进行二维傅立叶反变换，就可以得到f(x,y)。三维投影定理：令f(x,y,z)表示一个三维物体，它的三维傅立叶变换为如ω=0其中gz(x,y)正是f(x,y,z)在(x,y)平面上的投影，即表明f(x,y,z)在(x,y)平面上投影的傅立叶变换＝＝f(x,y,z)的三维傅立叶变换F(u,v,ω)在ω=0平面上的切面F(u,v,0)。与(x,y)平面成夹角为θ的平面上投影的傅立叶变换＝＝三维傅立叶变换F(u,v,ω)在与(u,v)平面成θ角的切面F(u,v,θ)。7.3傅立叶投影重建利用傅立叶变换的共轭对称性，积分限由0～2π换成0～π，R→|R|，积分限由0～∞换成－∞～＋∞，上式：记傅立叶投影重建图像为：以上是理想的情况－－可以获得无穷多个投影，对连续图像的傅立叶重建。如果只有有限个角度的投影g(ρ,θn)，θn表示nθ，G(R,θ)可用在一系列采样点(m△s，θn)上对g(•)求和得到，△s为沿着射线方向采样点的间距，采样点数为M，式(7.14)可写成：令R=k△R，k为整数，△R为频率域上采样间距，采样点数为M，取则有根据极坐标上点(k△R,n△θ)的值G(k△R,θn)插值出在直角坐标上点(k△u,n△v)的值F(k△u,n△v)，从而反傅立叶变换得到f(k△x,n△y)。7.4卷积逆投影重建由(7.17)可知：卷积逆投影法重建图像为：由式（7.24）可知，右边正是投影数据g(ρ,θ)与脉冲响应h(ρ)所表示的滤波器的卷积，h(·)为卷积函数。求f’(x,y,θ)则是在θ角方向上卷积了的投影，因此从式（7.22）求f(x,y)可被认为是求逆投影过程，即卷积逆投影重建法。用极坐标表示，用离散值代替连续积分，则式(7.23)可以写成：用极坐标和直角坐标之间的关系，求出与极坐标点相对应的直角坐标系上的点，从而得到用离散值表示的，最后，根据求逆投影式(6.22)得到重建的图像：(7.27)和(7.28)是一组便于计算机快速运算的表达式。7.5代数重建7.6三维图像重建的体绘制体绘制方法中最常见的有两种：（1）图像空间扫描的体绘制法：如图，从图像空间到物体空间的方法。7.7三维图像重建的面绘制