 预览加载中,请您耐心等待几秒...
预览加载中,请您耐心等待几秒...

1/10
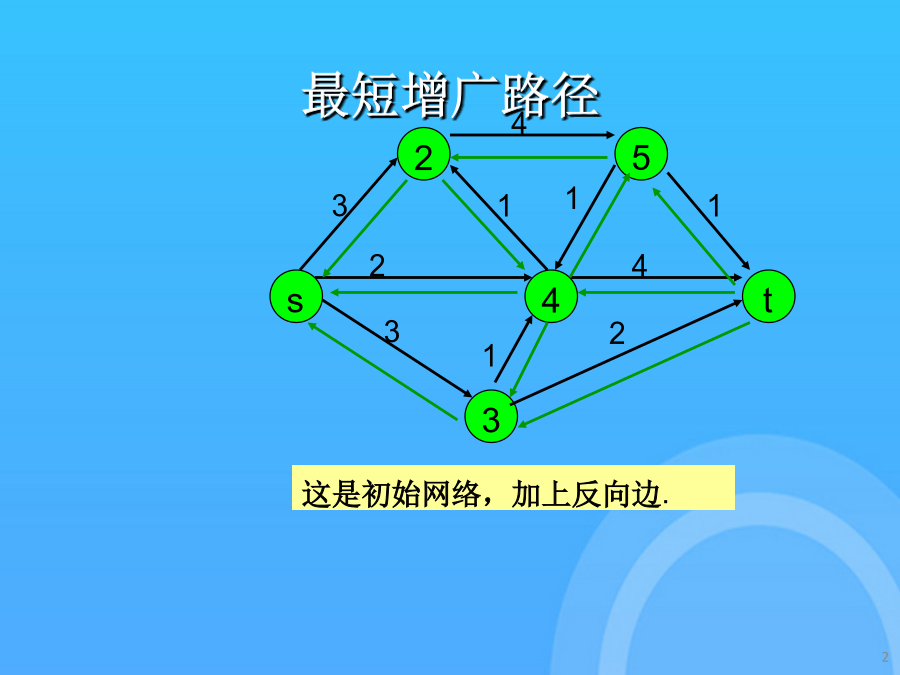
2/10
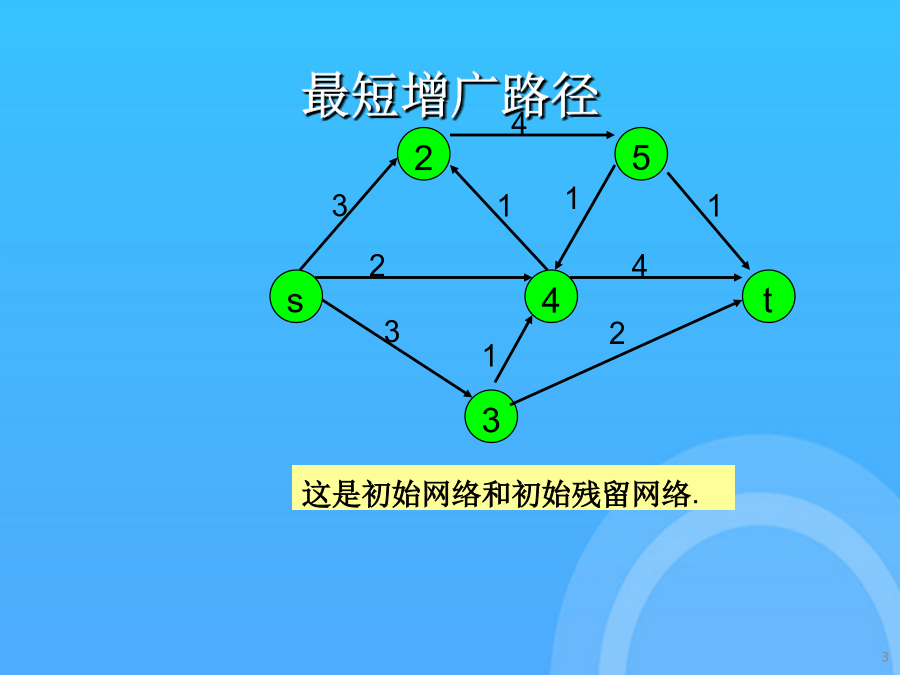
3/10
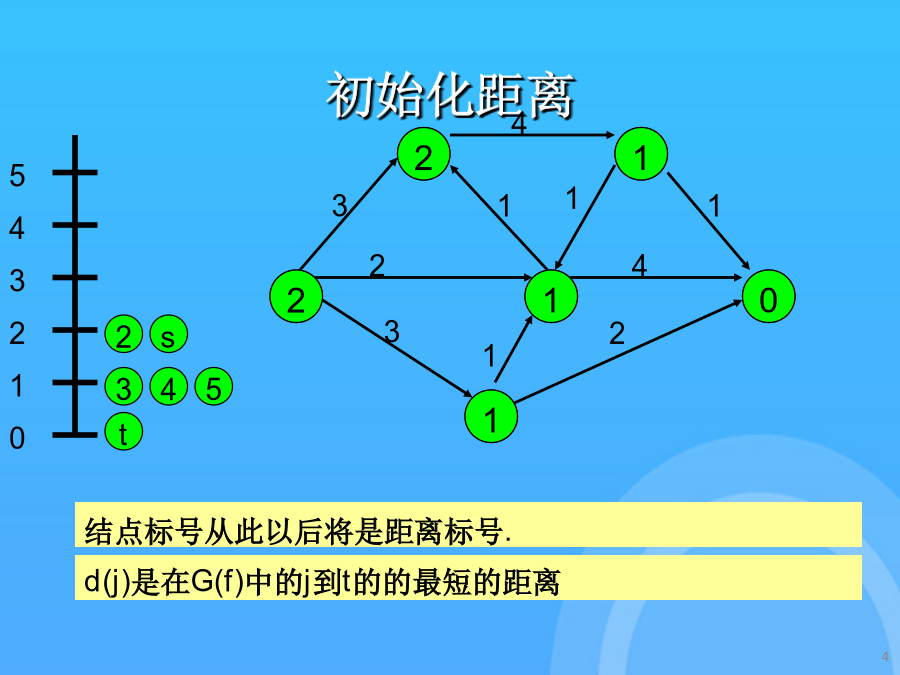
4/10
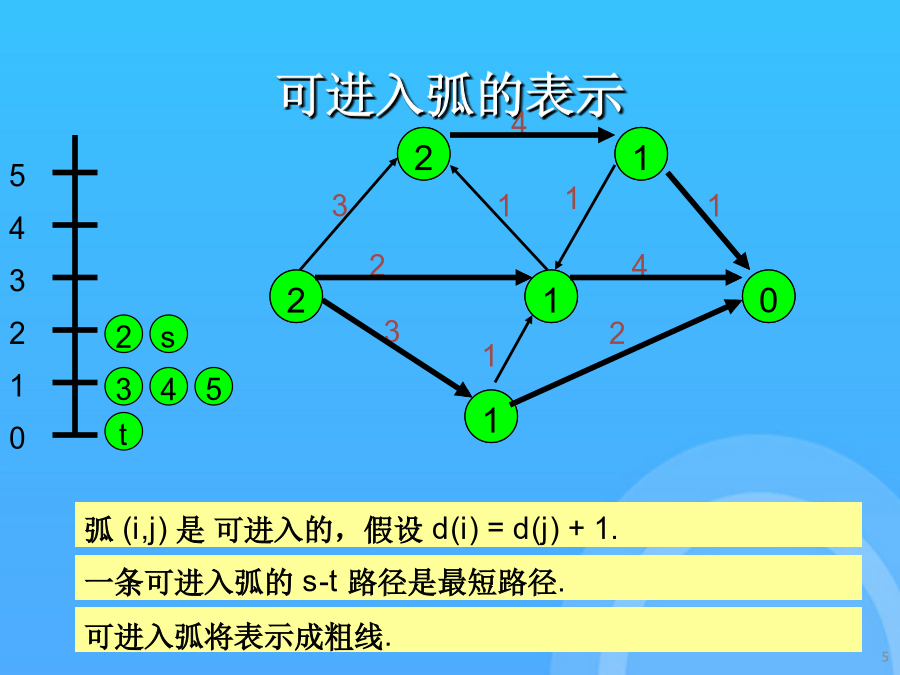
5/10
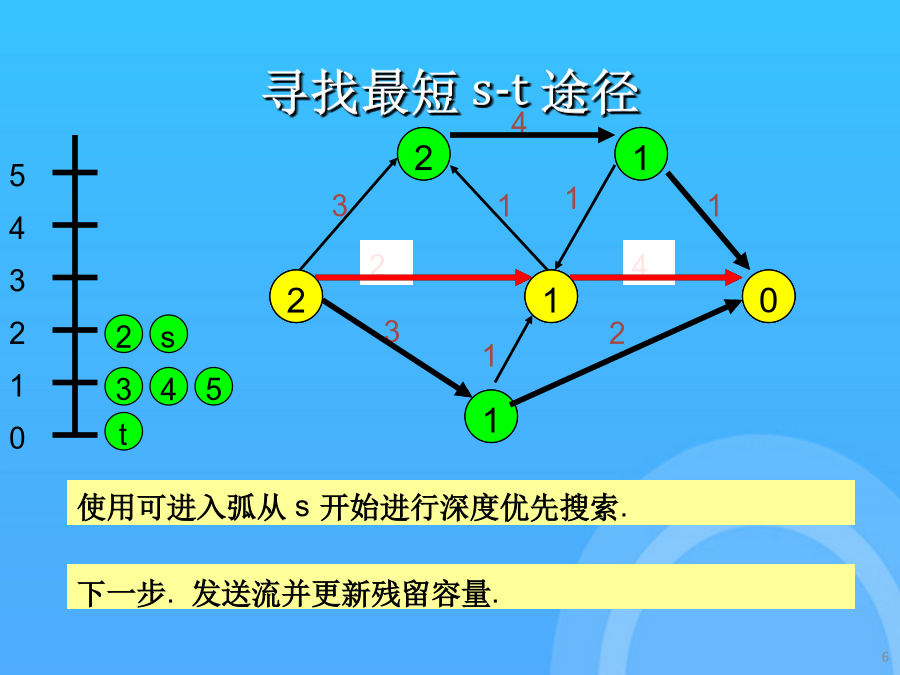
6/10
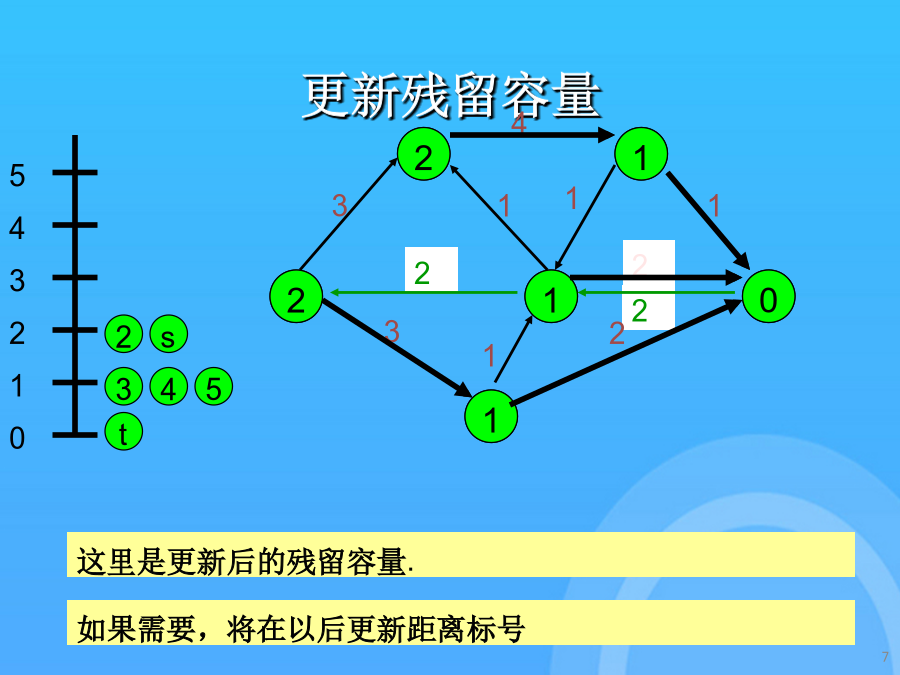
7/10
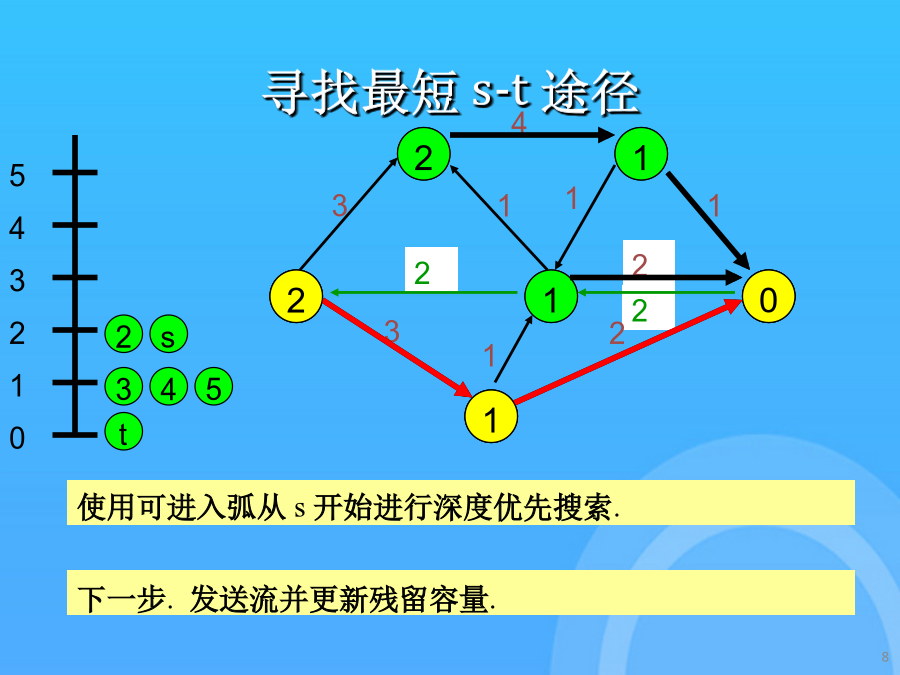
8/10
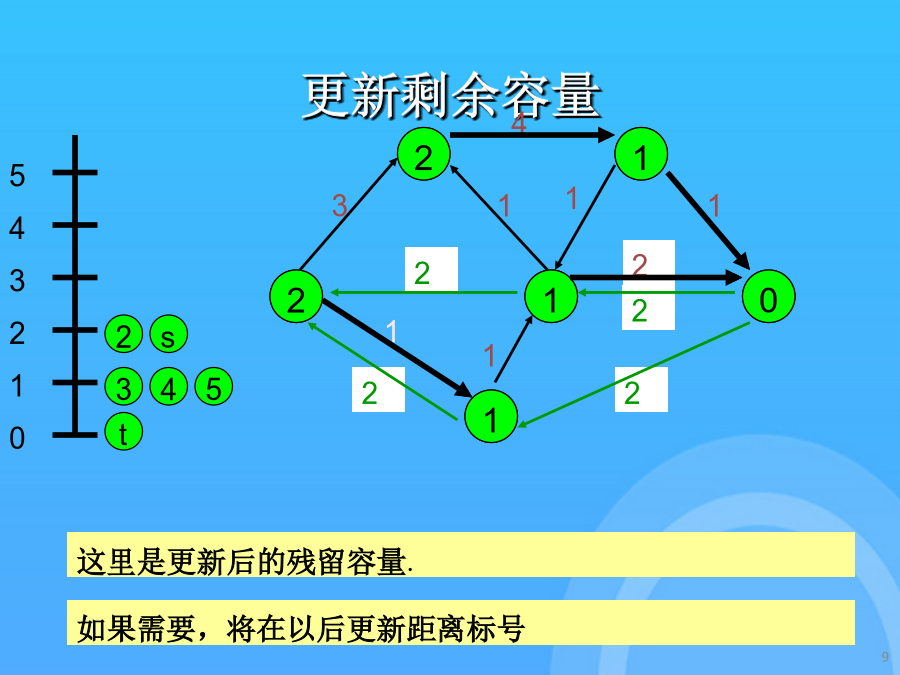
9/10
10/10
亲,该文档总共23页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
如果您无法下载资料,请参考说明:
1、部分资料下载需要金币,请确保您的账户上有足够的金币
2、已购买过的文档,再次下载不重复扣费
3、资料包下载后请先用软件解压,在使用对应软件打开
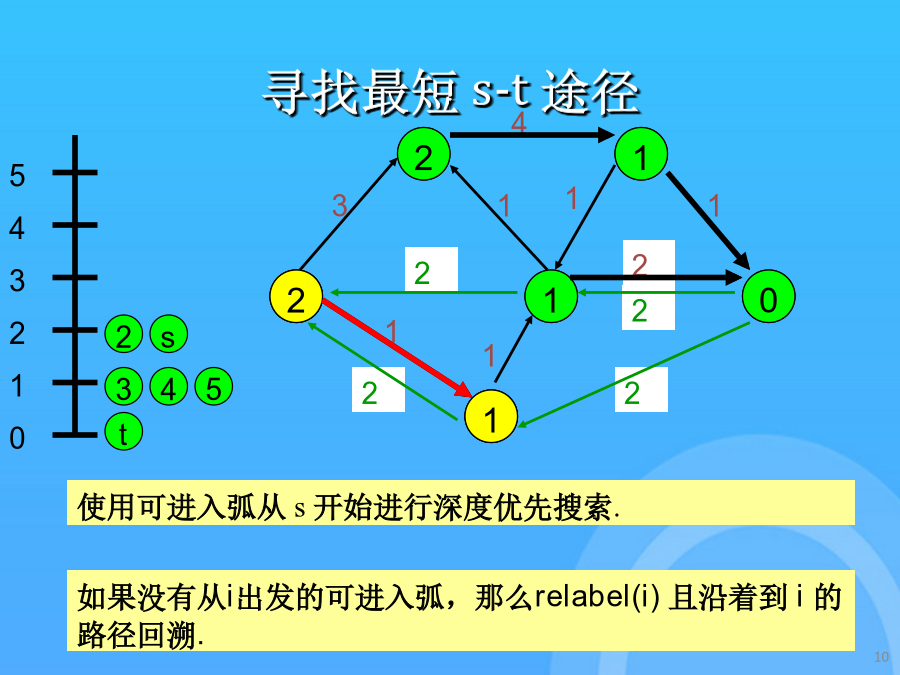
最短增广路径最短增广路径初始化距离可进入弧的表示寻找最短s-t途径更新残留容量寻找最短s-t途径更新剩余容量寻找最短s-t途径更新距离和路径如果没有从i出发的可进入弧,那么relabel(i)且反向沿着从s出发的路径的一条弧.可进入弧将表示成粗线.如果路径达到了t,那么发送流且更新剩余网络.这里是更新后的残留容量.如果需要,将在以后更新距离标号最大流问题的最短增广路径算法一条可进入弧的s-t路径是最短路径.残留网络中找不到s-t途径弧(i,j)是可进入的,假设d(i)=d(j)+1.得到最大流时的残留网络如果需要,将在以后更新距离标号d(j)是在G(f)中的j到t的的最短的距离发送流并更新残留容量.如果没有从i出发的可进入弧,那么relabel(i)且反向沿着从s出发的路径的一条弧.这是初始网络,加上反向边.寻找最短s-t途径更新残留容量搜索最短s-t途径搜索最短s-t途径搜索最短s-t途径更新残留容量这是初始网络,加上反向边.得到最大流时的残留网络使用可进入弧从s开始进行深度优先搜索.如果没有从i出发的可进入弧,那么relabel(i)且反向沿着从s出发的路径的一条弧.如果需要,将在以后更新距离标号一条可进入弧的s-t路径是最短路径.d(j)是在G(f)中的j到t的的最短的距离如果没有从i出发的可进入弧,那么relabel(i)且反向沿着从s出发的路径的一条弧.假设d(s)>n-1,那么没有从s到t的路径d(j)是在G(f)中的j到t的的最短的距离使用可进入弧从s开始进行深度优先搜索.搜索最短s-t途径弧(i,j)是可进入的,假设d(i)=d(j)+1.发送流并更新残留容量.寻找最短s-t途径得到最大流时的残留网络结点标号从此以后将是距离标号.更新残留容量搜索最短s-t途径得到最大流时的残留网络谢谢
















