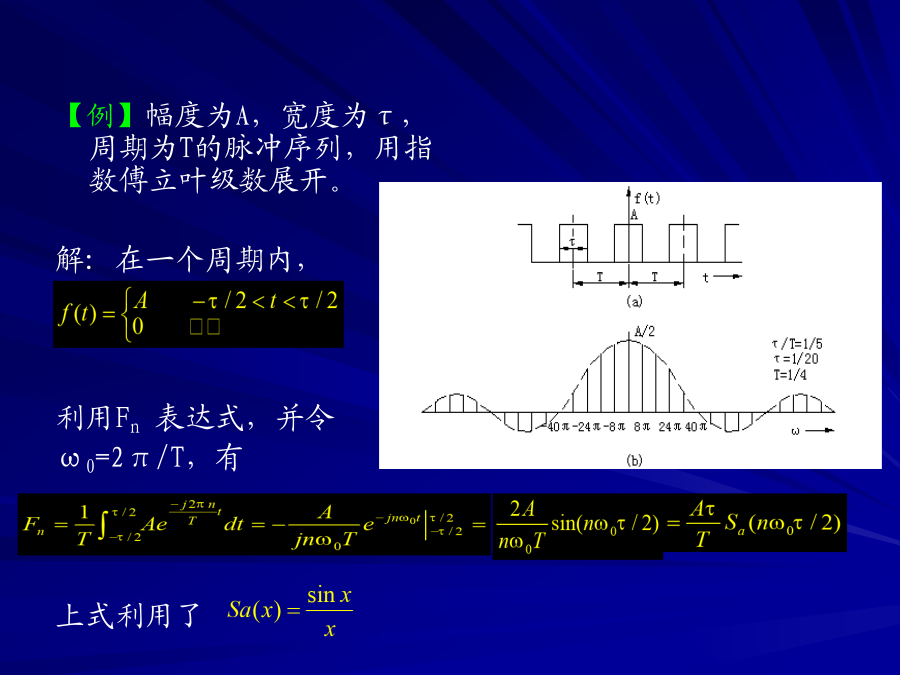
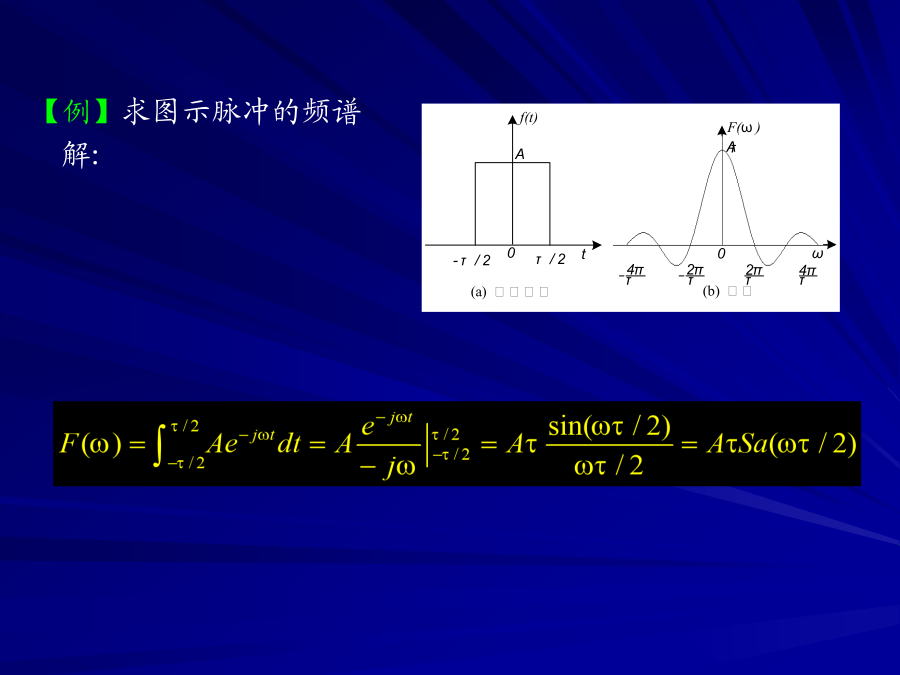
第2章信号分析指数形式的傅立叶级数式中【例】幅度为A，宽度为τ，周期为T的脉冲序列，用指数傅立叶级数展开。解:在一个周期内，利用Fn表达式，并令ω0=2π/T，有上式利用了给定周期信号f(t)，可以确定它的频谱；反之亦然。一般，Fn是一个复数。由Fn确定f(t)第n次谐波的幅度，它与频率之间的关系图形称为信号的幅度频谱。它不连续，仅存在于ω0的整数倍处，称为离散频谱。2.傅立叶变换非周期性信号，即傅立叶变换式。叫做的频谱密度函数，简称频谱。与是一一对应的关系。给定后，便是确定的；反之亦然。由求的过程叫做傅立叶（正）变换，而由求的过程称为傅立叶反变换。与组成傅立叶变换对，记作一般，如果在每个有限区间都满足狄里赫利条件，且下式成立，则其傅立叶变换存在。这是充分条件而不是必要条件。有些信号并不满足这些条件，但它们存在傅立叶变换。例如冲激函数δ(t)。【例】求图示脉冲的频谱解:【例】求图所示信号的傅立叶变换。解:－单位冲激函数或狄拉克函数。设是一个在处连续的任意函数，与乘积的积分称为单位冲激函数的筛选性质或抽样性质。求2.2信号的能量谱密度与功率谱密度1.能量谱密度（1）能量信号一个有界的、持续时间有限的信号，信号能量为有限值，全部时间的平均功率为零，这种信号叫做能量信号。通常把能量信号的归一化能量（简称能量）定义为由电压加于单位电阻(或电流通过单位电阻)所耗散的能量，即设能量信号的频谱为，则交换积分次序对于实函数所以（2）能量谱密度对上式中的，定义叫的能量谱密度。能量上式表明，信号的能量等于曲线下的总面积。故是能量密度的测度，单位为焦耳/赫，它代表信号能量沿频率轴的分布。实信号是的偶函数，因此2.功率谱密度（1）功率信号周期信号在的全部时间内存在，因此它有无限的能量，但平均功率为有限值，这种信号叫做功率信号。通常把周期信号在单位电阻上所消耗功率的平均值称为周期信号的归一化平均功率，简称功率。周期为的周期信号，其瞬时功率等于，在周期内的平均功率－的复共轭，结论：周期信号的归一化平均功率（总功率）值等于信号所有谐波分量幅度的平方之和，即等于各个频率分量单独贡献出的功率之和。（2）功率谱密度如果为时间无限的信号，若用代表在区间上的截短函数只要T为有限值，就具有有限的能量。设能量平均功率当，趋于一个极限，将它定义为信号的功率谱密度，用符号表示2．3卷积与相关1.卷积卷积表述对两个（或多个）函数之积进行变换的运算法则，（1)卷积积分给定两个函数和，定义积分叫做和的卷积。表示为包含冲激函数的卷积函数和单位冲激函数的卷积得出函数本身，推广：(1)(2)(3)卷积定理1）时间卷积定理若，，则2）频率卷积定理若，，则结论：时域中两函数的卷积等效于在频域中它们频谱的乘积；时域中两个函数的乘积等效于在频域中它们频谱的卷积。2.相关信号之间相似性或关联性的一种测度。设两个信号和，定义叫相关积分。和不同，是互相关积分。和相同，是自相关积分，对于实信号，,（1）相关定理1）时域相关定理若，则是信号的能量谱密度。结论：能量信号的自相关函数与其能量谱互为傅立叶变换。对于功率信号结论：功率信号的功率谱与其自相关函数互为傅立叶变换。2）频域相关定理若，则（2）自相关函数的性质1）能量信号的自相关函数R(0)等于信号的能量2）对所有τ有－系统的传输函数。无失真传输无失真系统的传输函数相移系统的带宽－|H(ω)|最大值的倍(3db)之间的频率范围，即ω2-ω1。2．5随机信号分析随机信号：信号参数不确定，不能预先确定信号在任意时刻的取值，取值具有随机性。例如话音信号、计算机产生的“1”、“0”序列等都是随机的。消息信号在接收之前，无法确切知道其波形。系统存在噪声或干扰，这也使得传输信号具有随机性。1.随机过程的概念无数台性能相同的接收机的波形n1(t)、n2(t)、n3(t)、……、nN(t)。每条曲线都是一个随机起伏的时间函数，称为随机函数。无穷多随机函数的总体在统计学中称为随机过程，随机过程中每一个随机函数叫做随机过程的一次实现或样本函数。在某一特定时刻t1观察各台接收机的输出噪声，它们的值不同。时刻t1是一个随机量。同样，时刻t2是另一个随机量。时间不同，随机量也不同，即随机量是一个变量，称为随机变量，它是时间的函数。随机过程的含义：①它是一个时间函数；②每个时