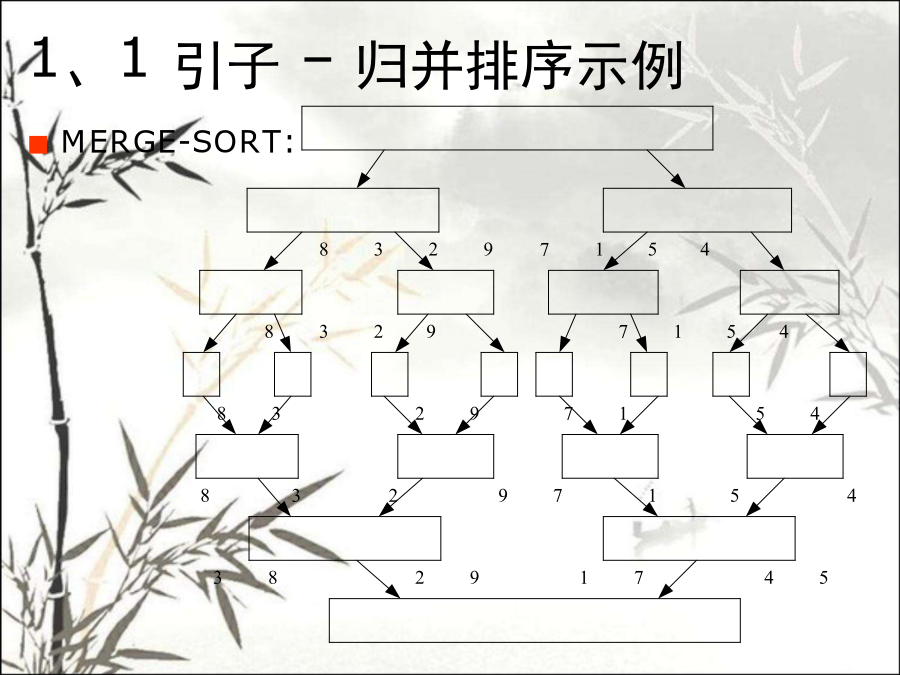
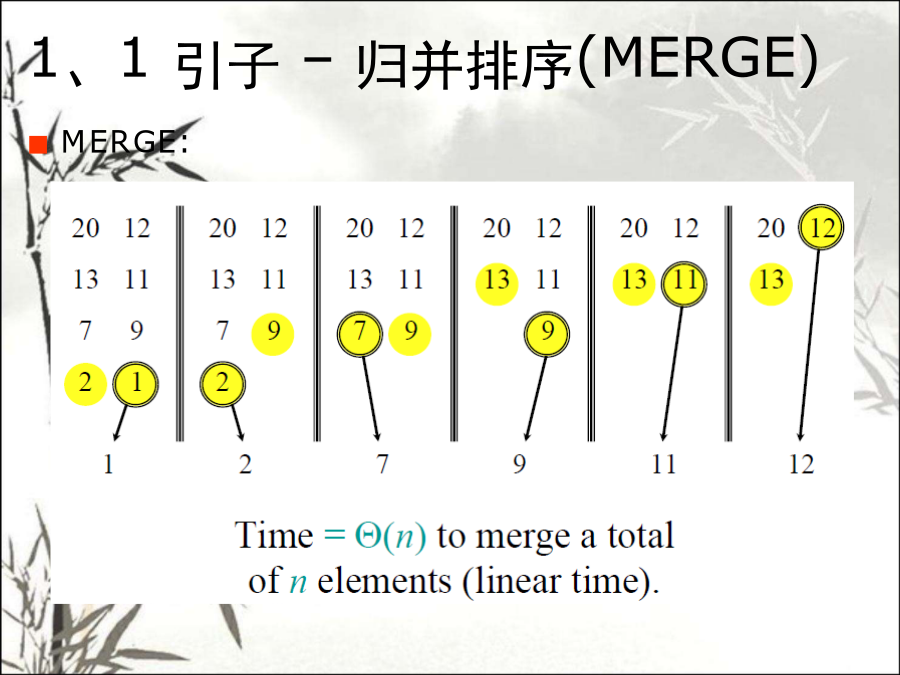
算法及其基础本章得要点与难点1、1引子–排序问题1、1引子–插入排序1、1引子–插入排序1、1引子–插入排序1、1引子–插入排序1、1引子–归并排序1、1引子–归并排序示例1、1引子–归并排序(MERGE)1、1引子–归并排序1、1引子–归并排序大家学习辛苦了，还是要坚持算法(Algorithm):对于计算机科学来说,算法指得就是对特定问题求解步骤得一种描述,就是若干条指令得有穷序列。算法得特性:输入(0个或多个)、输出(至少1个)、确定性(无歧义)、有限性、可行性。描述方式:自然语言、图形、程序设计语言、伪代码本书采用了面向对象程序设计语言C++,讲授时采用伪代码。算法与程序得区别？程序(Program)程序就是算法用某种程序设计语言得具体实现;程序可以不满足算法得性质(4)。例如:操作系统就是一个在无限循环中执行得程序,因而其不就是一个算法;操作系统得各种任务:可看成就是单独得问题,每一个问题由操作系统中得一个子程序通过特定得算法来实现。会场安排问题、单源最短路径、哈夫曼编码、最小生成树排序与查找、循环赛日程表最长公共子序列、矩阵连乘、凸多边形最优三角剖分、加工顺序等N后、最大团、图得m着色0-1背包、TSP、布线问题等等1、2算法得基本概念–拼图游戏在n×n格得棋盘上放置彼此不受攻击得n个皇后:按照国际象棋得规则,皇后可以攻击与之处在同一行或同一列或同一斜线上得棋子;n后问题等价于在n×n格得棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。1、2算法得基本概念–0-1背包问题起点1、3算法设计得一般过程算法复杂性(亦称算法复杂度)为算法运行时所需计算机资源得度量:时间复杂性(影响因素包括问题规模n、输入序列I、算法本身A):T(n,I,A)T(n)空间复杂性(影响因素包括输入输出数据IO、辅助变量V、算法本身A):S(IO,V,A)S(V)很显然:算法所需资源越多,算法得复杂性就越高;算法所需资源越少,算法得复杂性就越低。算法分析:对算法得时间复杂性和空间复杂性进行分析,这里主要还就是指对算法得时间复杂性得分析。方法:事后统计和事前分析算法分析得意义:算法设计:复杂性尽可能得低;算法选用:选择复杂性最低得算法;算法改进:算法分析有助于算法得改进。影响算法运行时间得因素(除算法本身外):机器;采用语言及编译程序;编程能力等。算法分析无需具体时间(精确或近似):针对同一问题不同算法得比较,相对而非绝对;应该独立于机器及实现语言;无论科技如何发展,其运行时间得测度应始终成立;关心得就是大得问题规模时得运行情况。渐近复杂性算法渐近复杂性态:设算法得运行时间为T(n),如果存在T*(n),使得就称T*(n)为算法得渐近性态或渐近时间复杂性。假设算法A得运行时间表达式为T1(n):T1(n)=30n4+20n3+40n2+46n+100T*1(n)≈n4(阶)假设算法B得运行时间表达式为T2(n):T2(n)=1000n3+50n2+78n+10T*2(n)≈n3(阶)渐近意义下得记号:O、Ω、Θ渐近上界-O(bigo)渐近下界-Ω(bigω)渐近精确界-Θ(bigθ)o、ω和θ渐近上界-O(bigo):设f(N)和g(N)就是定义在正数集上得正函数,下同。定义:如果存在正得常数C和自然数N0,使得当NN0时有f(N)Cg(N),则称函数f(N)当N充分大时上有界,且g(N)就是她得一个上界,记为f(N)=O(g(N))。即f(N)得阶不高于g(N)得阶。求T(n)=10n+4得渐近上界O:O(n)根据O得定义,容易证明她有如下运算规则:(1)O(f)+O(g)=O(max(f,g));(2)O(f)+O(g)=O(f+g);(3)O(f)O(g)=O(fg);(4)如g(N)=O(f(N)),则(f)+O(g)=O(f);(5)O(cf(N))=O(f(N)),其中c就是一个正得常数;(6)f=O(f)。常见得几类算法复杂性:O(1):常数阶;O(log2n),O(nlog2n):对数阶;O(n),O(n2),O(n3),…,O(nm):多项式阶。多项式时间算法;O(2n),O(n!),O(nn):指数阶。指数时间算法。几类复杂性之间得关系:O(1)<O(log2n)<O(n)<O(nlog2n)<O(n)<O(n2)<O(n3)<…<O(nm)<O(2n)<O(n!)<O(nn)Ω(bigomega):如存在正得常数c和自然数n0,使得当nn0时有f(n)cg(n),则称函数f(n)当n充分大时下有界,且g(n)就是她得一个下界,