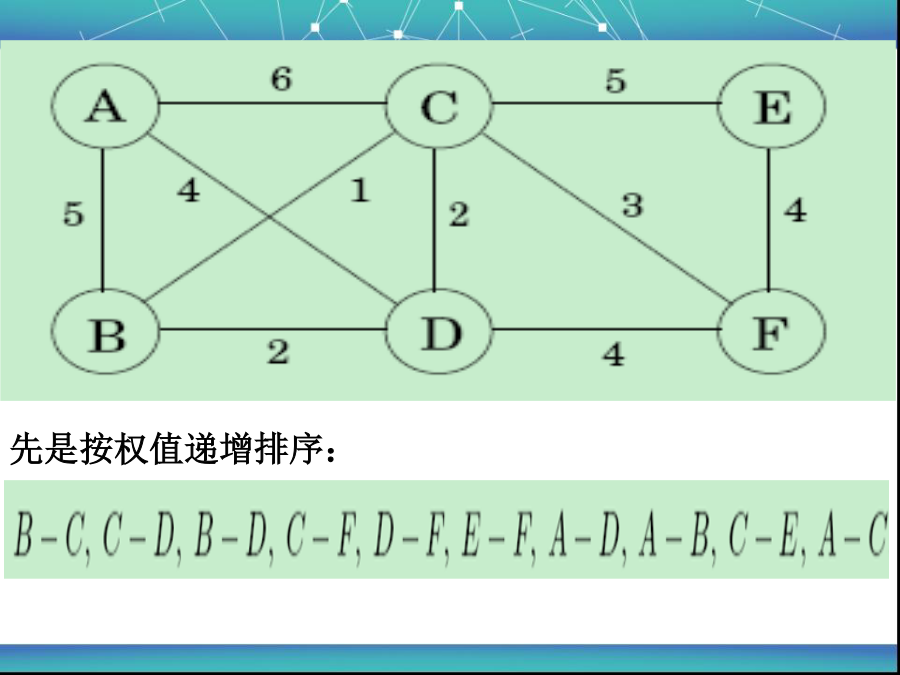
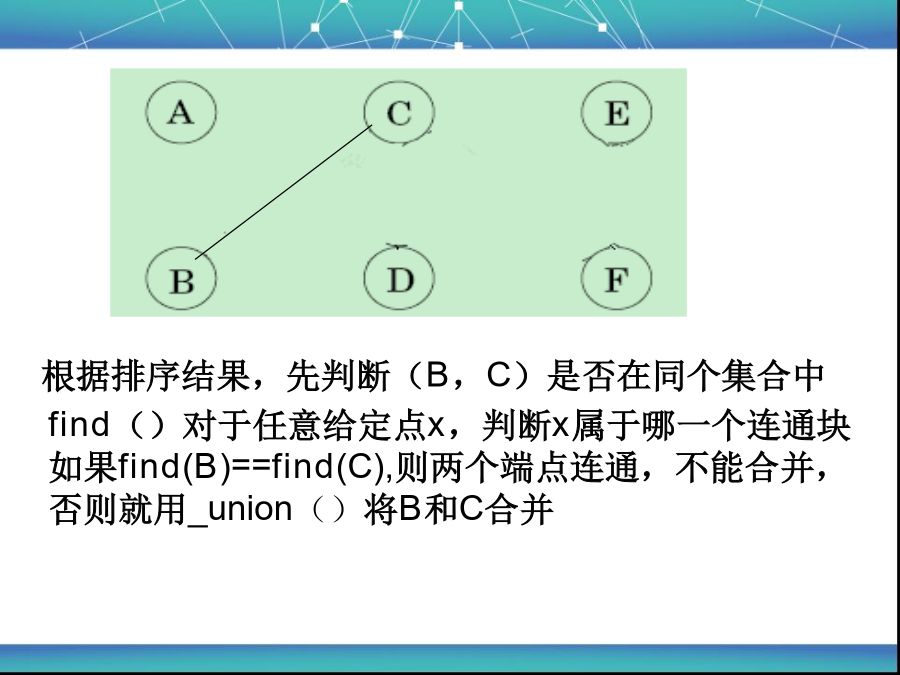
Kruskal算法算法过程：1.将图各边按照权值进行排序2.将图遍历一次，找出权值最小的边，（条件：此次找出的边不能和已加入最小生成树集合的边构成环），若符合条件，则加入最小生成树的集合中。不符合条件则继续遍历图，寻找下一个最小权值的边。3.递归重复步骤1，直到找出n-1条边为止（如果图有n个结点，那么最小生成树的边数应为n-1条），算法结束。得到的就是此图的最小生成树。typedefstruct{chara;charb;intweight;}edgenode;用快排对输入的边进行排序int_find(intx)//压缩路径的find（）{inty,z;y=x;while(parent[y]>=0)y=parent[y];while(x!=y){z=parent[x];parent[x]=y;x=z;}returny;}intkruskal(intn,intm)//n条边，m个顶点{inti,total,x,y;for(i=0;i<m;i++){parent[i]=-1;//初始化，先使每个节点各自形成一个单元素集合}for(i=1;i<n;i++){x=_find(graph[i].a-'A');y=_find(graph[i].b-'A');if(x!=y)//若边的两个顶点不属于同一个集合{_union(x,y);//就合并两个集合total+=graph[i].weight;//加上这条边的权值}}returntotal;}先是按权值递增排序：对各节点进行初始化（parent[i]=-1），使每个节点都属于单元素集合根据排序结果，先判断（B，C）是否在同个集合中谢谢！