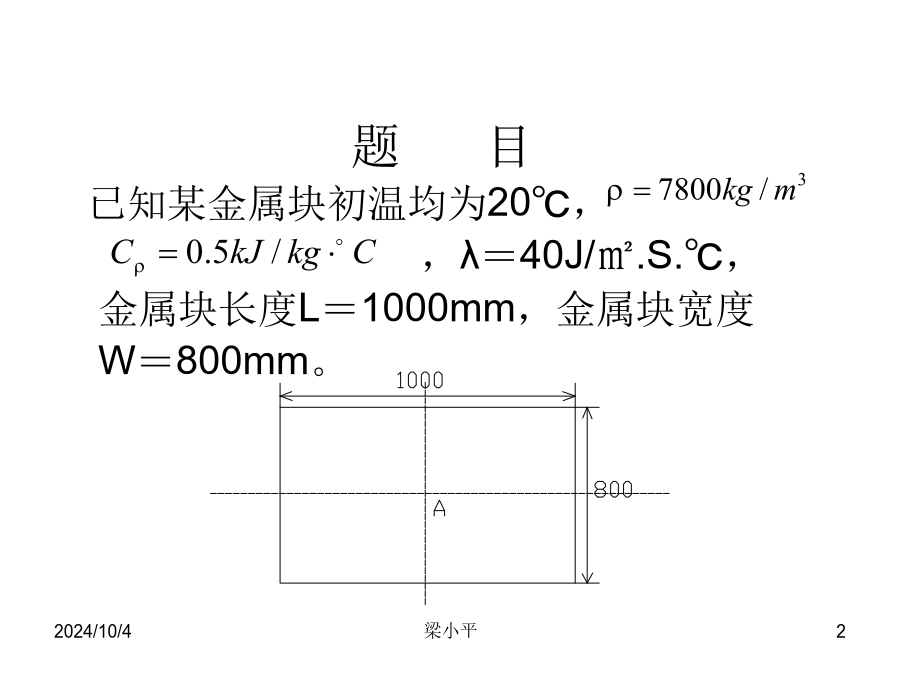
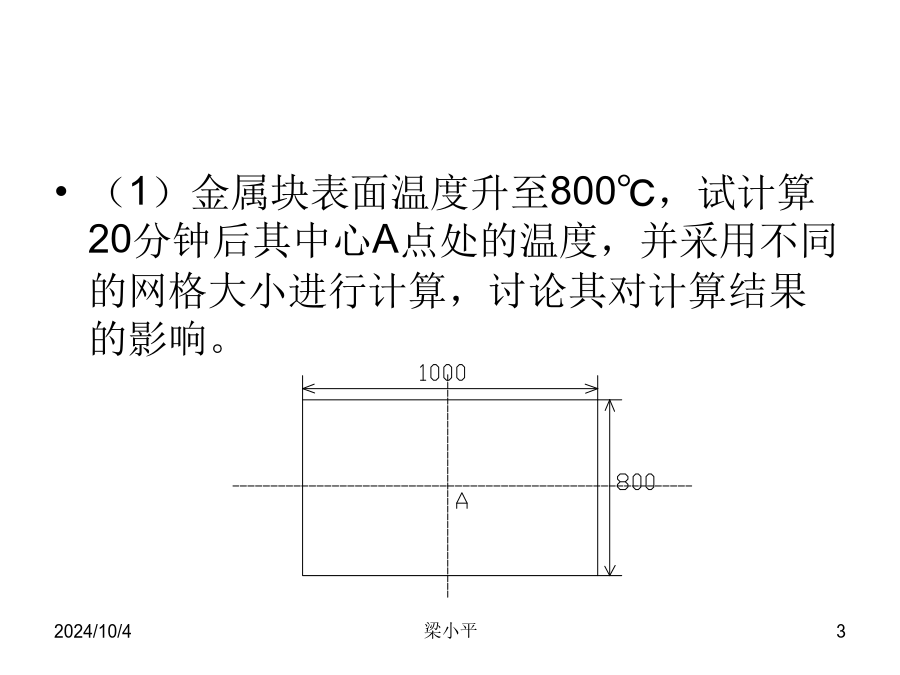
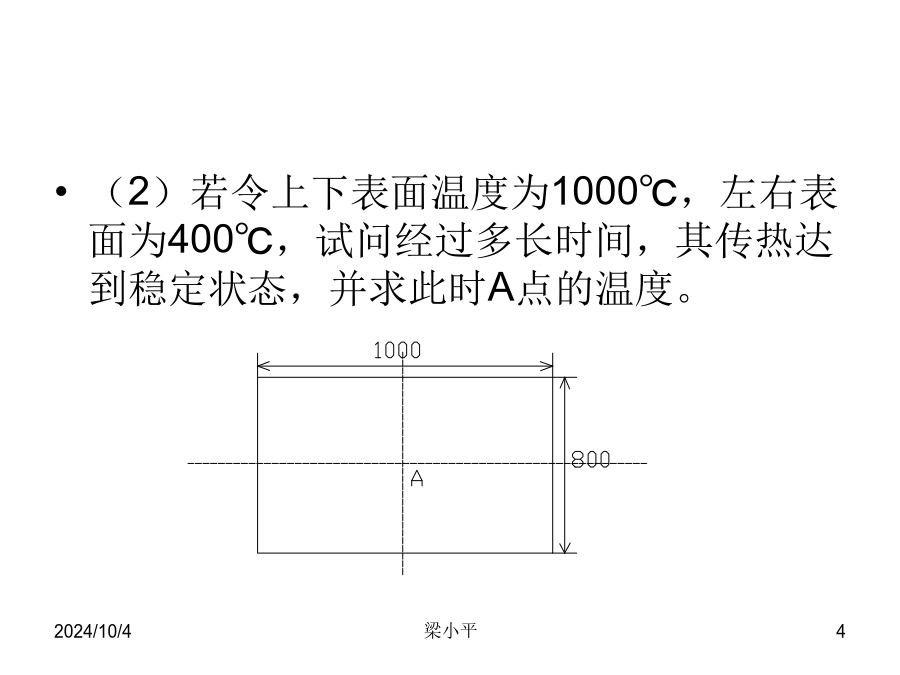
上机作业1题目（1）金属块表面温度升至800℃，试计算20分钟后其中心A点处的温度，并采用不同的网格大小进行计算，讨论其对计算结果的影响。（2）若令上下表面温度为1000℃，左右表面为400℃，试问经过多长时间，其传热达到稳定状态，并求此时A点的温度。一、求解区域离散化二、计算方程的建立二、计算方程的建立划分网格判断是否符合稳定性条件，是则继续；否则重新划分网格赋各节点初值（内部及边界节点）计算下一时刻各节点的温度判断是否结束计算是则输出结果，否则以新值作为初始值再计算下一时刻的各点温度上机作业2题目同前，边界条件与第2问相同（即上下表面温度为1000°C，左右表面温度为400°C，试用隐式差分方程求解达到稳态后的中心A点的温度。一、隐式差分方程的建立略二、隐式差分方程的迭代计算一、隐式差分方程的建立一、隐式差分方程的建立划分网格赋各节点温度值（内部节点赋假设值，边界节点赋已知值）根据方程计算各节点温度新值计算假设值与新值之差即误差判断误差是否小于规定值，是则输出结果，否则以新值作为假设值再重新计算各点温度新值